dimensionless
flow versus breach experiment geometry parametersMay 20, 2001 - Begin work and review of reference texts to understand principles of the flow of water through weirs.
May 27, 2001 - plots of dimensionless
flow versus breach experiment geometry parameters
May 31 - June 1, 2001 - Fit 
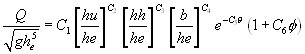to 16-inch data with simulated annealing
June 1, 2001 - Fit 
with simulated
annealing
June 4, 2001 - Test the then-widely-accepted National
Weather Service BREACH model equation by Dr. Danny Fread, 
, against Mr. Temple's entire data set and find
a very strong dependence upon theta. Question: What if there are
two kinds of flow, based upon bhe1.5 and he2.5?
That might imply a simple weighted equation, 
June 5, 2001 - Make minor corrections to Mr. Temple's experimental flume data for plywood breaches with 16-inch gap at base. Set up simulated annealing program, simana2.for to fit simple weighted equation to it. Meeting with Dr. Mitch Neilson, Kansas State University.
June 6, 2001 - Sort 16-inch data into sets of separate
geometries for plotting C1 and w versus geometric parameters
from simulated annealing fits to . Reason
that the data for headcuts, hh, of 1 ft and small theta have the
best chance of producing flow into the headcut slot from the sides.
June 7-8, 2001 - Examined 35mm slides of the breach
experiments to find obvious evidence of flow controlled by the
topmost geometric edges of the plywood breach models. See HERU
slides 148957 and 148958. Integrated ideal weir equation 
along the geometric edges of the experimental plywood
model to obtain trial equation 
to
fit to the 16-inch plywood breach model data. Plot parameters
Cd, Cc and w as functions of geometric parameters. Find that Cd
and Cc are strongly dependent upon the upstream slope angle
of the "dam", theta, contrary to Mr. Temple's predictions.
Started sorting 16-inch data into subsets according to headcut
height, hh, for separate fitting by simulated annealing.
June 19, 2001 - Use simulated annealing to fit a0 and
a1 in 
to individual breach geometries, and then plot
with SPSS TableCurve 3-D against breach geometry parameters, using
various user-defined trial functions for theta versus fi. Justifies
the use of the upstream slope of the plywood dam due to an obvious
dependence of both a-coefficients upon theta. As Mr. Temple predicted
would not happen and demanded to see proven.
June 20, 2001 - One month after starting work. Using
simulated annealing to fit equation
and
figure out what dependence remains upon breach geometric parameters.
July 6 - 12, 2001 Using simulated annealing to fit higher
order equations to 16-inch gap plywood model data, with hh = 1,
up to 
, which produced an average relative error (percent
of calculation versus measurement) of 3.96%. By means of comparison,
Mr. Sappington's notes estimating his measurement error during
the flume experiments appear taped to the top of the left page
in my Lab Notebook on July 16, 2001. Then and only then did I
begin to work with Dr. Hanson on his project, with Mr. Temple's
explicit permission. The values of the fitted coefficients, although
not to full precision and depending upon transcription errors,
are:
a0 = 3.87540, a1 = 0.11446, a2 = -0.35048, a3 = -0.29932, a4 = -0.0311276,
a5 = 0.24912, b0 = 7.42012, b1 = 0.34232, b2 = -1.7178, b3 = 0.019247,
b4 = 0.104268, b5 = 1.16042
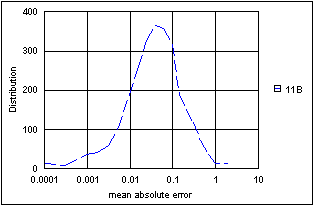
Note - Since this fit is only for hh = 1 and it does not account for all effects, it does not fit the rest of the flume experiment data as well. Most of the simulated annealing fits made in 2001-2002 used the cumulative relative error (defined on page 25, June 5, 2001) or the mean relative error as the objective function (function to be minimized by the fit). This is a percentage of calculation error, which produces lower errors in smaller calculated values and higher errors in higher calculated than other common measures, such as sum-squared-error which targets the largest possible errors. In more recent work, I've used the mean absolute error, which tends to be have a log-normal distribution and produces smaller relative errors for the more important larger flows in this problem. A recent June 13, 2007 such fit of an equivalent equation to the same data as June 12, 2001 produced:
mean absolute error = 0.0717173 CFS, standard dev of error = 0.1081 CFS
mean relative error = 4.579%, std dev of relative error = 4.957%
a0 = 0.68669, a1 = 0.20259, a2 = -0.037235, a3 = -0.20065, a4 = -0.028911
a5 = 0.041575, b0 = 0.44260, b1 = -0.78288, b2 = -0.46517, b3 = 0.11677,
b4 = 0.083613, b5 = 0.26533
May 14 - June 11, 2007 - Redo old work, under medication, developing new equations. Final fit to the entire set of Mr. Temple's data, all 8, 16 and 32 inch data:
, with
Q(hat) = calculated breach flow, cfs or ft3/s
b = bottom width of gap in plywood breach, ft
g = acceleration of gravity, 32.174 ft/s2
he = height above the verge of the breach (b) of water upstream, ft
hh = depth of headcut below verge of breach (b), ft
ms = slope of the side of the trapezoidal breach cut, horizontal to vertical, dimensionless
mu = slope of the upstream side of the plywood dam, H:V, dimensionless
D1 = 0.46342, D2 = 0.32459, D3 = -0.16306, D4 = 0.51441, D5 = 8.6838,
D6 = -0.10813, D7 = 0.73077, D8 = 0.50789, D9 = 2.5213, D10 = 0.38428
mean absolute error = 0.08304 CFS
standard deviation of absolute error = 0.13877 CFS
mean relative error = 4.91%, std dev of relative error = 5.94%
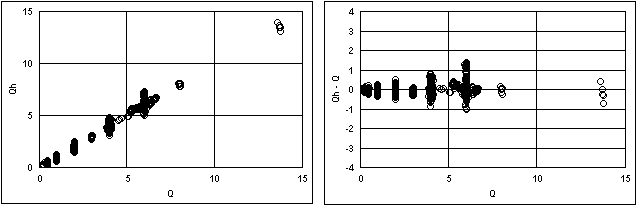
Qh = calculated flow, cfs
Let he who would cast the first stone damn well do a better job.