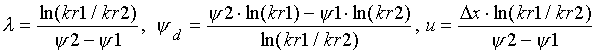This investigator found that the composite conductivity relation is simply too complex to be useful in discovering the mathematical nature of Darcian means so as to make suitable approximations to them in running models. It was more useful, by far, to begin with the simplest mean possible even if it does not initially seem of much practical use. For this approach, using one of the few explicit analytic expressions for Darcian means develops an analytic basis for further exploration.
Consider the exponential conductivity relation of the form [22]. Numerical solutions of the elliptic boundary conditions problem [11] will lead one quickly to suspect that kr(x) for this relation is of the form [23]. This can be verified by direct substitution into [11], and reduction to 0 = 0. By direct substitution and integration, one can also get [24] from [22] into [8], and [25] from [23] into [7]. One can also substitute [24] and [25] into [6], and by making the appropriate substitutions get [26].
[22]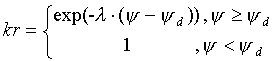 
, where
kr = unsaturated relative conductivity (dimensionless), l = fitting parameter (1/m), y = matric suction (m), and yd = displacement pressure (m).
[23] 
, where
a = kr1, b = 
, u = l
Dx , Dx = x2 – x1
[24]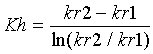 
[25]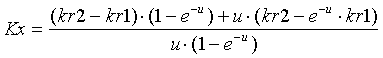 
[26]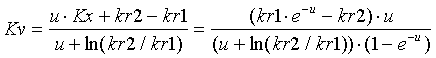 
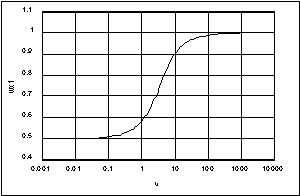
Suppose that we wish to do the usual thing and determine Kx as a weighted sum of kr1 and kr2 [27], and Kv as a similar weighted sum [28]. The weights, wx1 and wv1, are solved in [29] and [30], showing that wv1 à wx1 (Figure 17) as (kr1,kr2) goes to the kr1=kr2 diagonal. The reader will find it easier to verify these equations if he or she uses a symbolic math package, such as Maple V or Macsyma.
[27] 
[28] 
[29]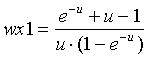 
[30]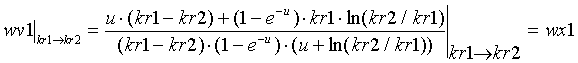 
, NOTE, I believe this equation is in error, click here for a more accurate form.
 |
|
|
It is apparent that 0.5 — wx1 — 1, which can be verified with a symbolic math package, or L’Hospital’s rule. For the purpose of scaling, we may wish to know the value of u for which wx1 = 0.75, the half point of the curve. If we rearrange [29], we get the implicit relation in [31], which can be solved for a universal constant for this kind of problem, u0.75.
[31]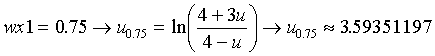 
Consider now the first derivative of [22] in [32], that allows us to solve for l in terms of the conductivity relation. If we substitute this into the definition for u in [23], we get [33], a definition for u in terms of the vertical space step size between adjacent cells and the conductivity relation. What would happen if we were to use this expression with the Brooks-Corey conductivity relation [34] and possibly a van Genuchten style relation [35]? We get the definitions for the associated u-parameters in [36] and [37]. We will find this useful later in scaling Darcian means for the Brooks-Corey relation.
[32]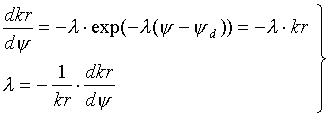 
[33]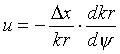 
[34]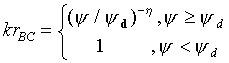 
[35]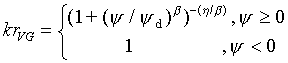 
[36]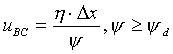 
[37]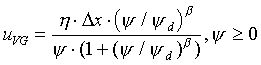 
There is some numerical verification that these forms are correct. Suppose that we solve [11] using the Brooks-Corey relation [34] (yd = 0.082m, h = 8.075) for some points very close to the kr1-kr2 diagonal, say about 0.2% off of it, and then back-calculate wx1 and wv1 from [27] and [28]. In Figure 18a wx1 and wv1 have been plotted for kr~kr1~kr2 varying from about 1 to about 8.5(10-42) in 48 log steps, and Dx varying over ten orders of magnitude. Note that the plots are all the same shape and seem to differ only by a uniform log step. Since y in [36] must also vary in log steps with kr, so does uBC. The plots for wx1 and wv1 in this regime plot directly on top of each other.
(To be honest, I cannot recall having verified the numerical fit of this data to [36], but the concept works so well, as we shall see, that I will pass on that detail in favor of finishing this report. - DLB)
Figure 18b shows a similar set of graphs plotted for [35], where yd = 0.082m, b = 4.23 and h = 8.075. Again the plots for wx1 and wv1 occupy the same positions for the same parameters. Note that the distribution of wx1 curves are no longer uniform. In fact, the curves begin in the middle range for highest kr (lowest y), plot to the left and then in a more uniform distribution to the right. Where scaling parameter, u, for the exponential and Brooks-Corey relations did not depend on yd, this does [37], in a much more complicated manner. This investigator has not as yet pursued study of Darcian means for the van Genuchten style relation [35], but it is apparent that the uniform distribution of wx1 plots to the right correspond to the asymptote for large y evident in [37].
Note that Figure 17 suffices for any similar set of graphs for [22]. In this simple case, u is not dependent on either kr or yd.
 |
 |
|
|
|
But this is not the only valid way to consider weighting and scaling Kx and Kv. Consider what we have learned from Figures 3a-f and 4a-f. Kv does not transform from kr1 to kr2 as Dx increases, it transforms from Kh to kr2. Likewise, Kx transforms from some prototypical Kx (for Dx à 0) to kr2. Might not weighted mean approximations, [38] or [39], for relations more complex than the exponential provide better accuracy on that basis?
[38] 
[39] 
We already know from [6] that as Dx à 0, Kv à Kh, [40] for the exponential relation. We can easily determine [41], which provides the weight formula [42] for wx0. The formula for wvo is much more complex, but reduces to [43], which is useful enough. The plot of [42] looks very much like the plot of [29], Figure 17, except that it rises from 0 to 1, with a midpoint at wxo = 0.5, where u = 3.593511696, the same universal constant as before.
[40]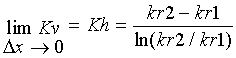 
[41] 
[42]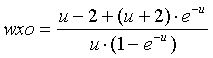 
[43] 
The reader will find that [29] and [42] provide some difficulties in computation over the full range of possible values, even with double precision variables in FORTRAN. Listings 1 and 2 offer compromise calculations that this investigator has found useful.
|
Listing 1: FORTRAN routine for [29] double precision function wd1 (u) |
Listing 2: FORTRAN routine for [42] double precision function wdo (u) |
Other than a convenient analytic example, of what general use are Darcian means derived for an exponential conductivity relation? If a reader plots an exponential relation in the same log-log space as a Brooks-Corey or van Genuchten relation, the reader will notice that the exponential relation curves downwards as matric suction increases to the right. The reader may also notice that such curvature might possibly approximate the curved part of a van Genuchten relation near saturation.
Since the exponential function [22] has only two parameters, it can be uniquely determined by two points in (y,kr)-space, say the two grid points in a model (Fig. 1). Taking those two points, we can solve for l, yd and u [44], defining the function of [22] that passes through the points and the appropriate scale for the weight. We will make use of this later.
[44] 