

Abstract
Previous work has demonstrated that using non-Darcian interblock conductivity means in mass-conservative models of unsaturated infiltration can produce mass infiltration errors up to twenty times larger than those that mass conservation corrected. But the method to generate true Darcian means from solutions to elliptic boundary condition problems is too computationally intensive to be used effectively in models, especially with variable porous media. A previously introduced approximation did not estimate Darcian means well near saturation for relations, such as a van-Genuchten form, with strong curvature away from the asymptote near saturation. This paper introduces a generally more accurate approximation to Darcian means, using the examples of matrix and fracture flow conductivity relations for Topopah Spring welded volcanic tuff (Yucca Mountain, Nevada, USA), and compares it to the geometric and arithmetic means for matrix and fracture flow, respectively. While the new Darcian Integral Mean approximation may have significant computational overhead of its own, compared to standard means, as well as imperfections, it offers to other investigators a reasonable tool to examine the properties of Darcian means in running models.
key words
Yucca Mountain tuff, unsaturated flow, numerical method, simulation model, elliptic boundary condition problem
Introduction
Warrick (1991) first showed that standard interblock hydraulic conductivity means in vertical unsaturated water flow in soil, such as the arithmetic, geometric and upstream, can produce non-Darcian flows in error by as much as 100 times. Baker (1995) confirmed Warrick's results for a wider range of soil conductivity relation parameters by switching from Warrick's integral derivation of Darcian means to a numerical elliptic boundary condition approach, and suggested the existence of a logistic weighting function to determine Darcian means from adjacent vertical grid cell conductivities. Baker (1998a) later discovered an analytic solution for Darcian means to the exponential conductivity relation, and showed how standard means could produce vertical interblock flow errors of up to six orders of magnitude, especially for imbibition.
Baker, et al., (1998b, in review) then demonstrated how the arithmetic mean can lose up to half of the mass infiltrated in a mass-conservative unsaturated infiltration model, due to non-Darcian interblock flows, at fixed vertical space step sizes much larger than the "displacement pressure". The size of this error is about 20 times larger than the mass infiltration error reduced by using a modern, mass-conservative method (Celia, et al., 1990). A simple, piecewise approximation to Darcian means in a mass-conservative model reduced the mass infiltration error size to less than 0.5%, over five orders in magnitude in vertical step size. This produced an improvement of up to two orders of magnitude over the arithmetic mean in the same model.
Unfortunately, the piecewise approximation depended on a straight line fit in the space of log relative conductivity versus log matric suction. It did not fit well near saturation in the case of Havercamp's test soil (Haverkamp, et al., 1977), where the van-Genuchten-style conductivity relation curved in that log-log space. That makes it necessary to consider a more exact approximation, which is presented here.
Darcian means provide a new mathematical and modeling framework by which modelers can judge the appropriateness of their approximations for interblock conductivity means. But the study of Darcian means is still evolving. At present, for an arbitrary relative conductivity relation without an analytic solution, the elliptic boundary condition approach is the most accurate method to develop true Darcian means. But it is currently so computationally intensive as to make it unsuitable for use in a running model. If one has a homogeneous porous medium, such as an engineered barrier, fixed throughout time and space, then it may be reasonable to use the elliptic boundary condition method to pre-calculate Darcian means over a range of cell conductivities and grid spacings. One could then use a lookup and interpolation table in the model. But if the medium is variable, then a more general method with reasonable computational overhead is necessary.
The character of Darcian means and the validity of using them in models has been adequately introduced in previous work. This paper will only compare the proposed integral approximation to the true Darcian mean for a limited set of cases, and offer it as a tool for other investigators to compare Darcian to standard means. Links to the data sets developed for this paper, the contours of some true Darcian means in the space of adjacent grid conductivities, can be found below in the section labeled Data Sets, between Conclusions and References. For a limited time, this data is also available at the Aquarius Engineering web site [1].
Expanding and Extending the Analytic Solution for an Exponential Relation
In a previous work (Baker, et al., 1998b, submitted), the true interblock Darcian mean, Kv, in vertical flow [1] for the exponential relative hydraulic conductivity relation [2] was expressed as [3]. The the similar mean for horizontal or diffusive flow, Kh, was expressed as [4], showing both the general and particular forms. Previously cited works have also shown that as the grid cell spacing, Dz, increases from much smaller than the "displacement pressure" in [2] to much greater, Kv(k1,k2,Dz) transforms from Kh to k2. If one postulates a Darcien weight, wv, in [5] and solves for it using the exponential relation analytic solution, one gets [6]. Listing 1 shows the FORTRAN code necessary to calculate wv [6], including code for the all the anticipated special conditions.
[1] ![]() ,
,
where Q = interblock flow (m/s), Ks = porous medium saturated flow (m/s), Kv = interblock relative conductivity mean (dimensionless), H = total hydraulic head at grid cell centers (m), z = positive upwards vertical position of cell centers (m), y = matric suction or negative pressure head (m). For this discussion, the lower cell has matric suction, y1(z1), at the center, z1, and the upper cell has y2(z2) at the center, where Dz = z2-z1.
[2] ![]() ,
,
where kr = unsaturated relative conductivity (dimensionless), l = fitting parameter (1/m), and yd = "displacement pressure" (m).
[3] ![]() ,
, 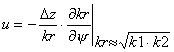 ,
,
where k1 = kr(y1), the relative unsaturated hydraulic conductivity at grid center at z1 (dimensionless), k2 = kr(y2), the relative conductivity at the vertically adjacent cell center at z2=z1+Dz, and u = Darcian scaling factor (dimensionless).
[4] ![]()
[5] ![]()
where Dk = k1-k2, rk = ln(k1/k2)
rk = dlog(k1/k2)
dk = k1-k2
eu = dexp(-u)
if (dabs(dk)/k2 .le. 1.d-4) then
if (u .le. 0.0036d0) then
wv = u/6.d0
else if (u .ge. 36.d0) then
wv = (u-2.d0)/u
else
wv = (u-2.d0+(u+2.d0)*eu)/(u*(1.d0-eu))
end if
else
if (u .le. 0.0036d0) then
wv = (dk*(1.d0+0.5d0*rk)-k1*rk)*u/(-rk*(dk-k2*rk))
else if (u .ge. 36.d0) then
wv = 1.d0 - k2*rk*rk/(u*(k1-k2*(1.d0+rk)))
else if (dabs(u-rk)/u .le. 1.d-4) then
wv = (dk*dk-k1*k2*rk*rk)/(dk*(dk-k2*rk))
else
wv = ( (1.d0-eu)*dk*(u-rk) +(k1*eu-k2)*rk*u) /
+ ( (1.d0-eu)*((dk-k2*rk)*u-dk*rk+k2*rk*rk) )
end if
end if
At the present time, there are no readily apparent analytic solutions for Darcian means for conductivity relations other than for [2] or simpler. Suppose that we hypothesize that [5] and [6] may apply to another relation, kr(y), if Kh is replaced in [5] by the integral form in [4] for the other relation. Let us call this the Darcian Integral Mean approximation, Ki [7]. In this case, let us consider van-Genuchten-style relations [8] for unsaturated fracture and matrix flow for Topopah Spring welded volcanic tuff. Let us use either expected values of the parameters reported in Schenker, et al. (1995), or their fits to suitable transformations from saturation relations to conductivity relations. In this case, we care only to distinguish between fracture and matrix flow in general, as a demonstration of Darcian means for two different media types, not to provide relations to fit any particular flow.
[7] ![]()
[8] 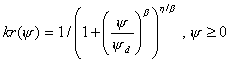 ,
,
where b and h are fitting parameters (dimensionless), with h corresponding to "pore size distribution index"; for fracture flow: yd = 0.082 m, b = 4.23, h = 8.075, and for matrix flow: yd = 33 m, b = 1.793, h = 1.9825.
To test the hypothesis, we use the elliptic boundary condition
method to generate true Darcian means, Kv, between vertically
adjacent grid cells, separated by center-to-center distance, Dz, to a flow uniformity of dr < 10-4
, over 512 fine-grid cells adaptively spaced over Dz,
with k1 and k2 used as boundary conditions, varying between 10-8
or 10-4 and 1. In this case, dr = (rqmax-rqmin)/Kv,
where rqmax is the maximum local relative flow, Q/Ks, between
any of the 512 fine-grid cells in the elliptic boundary condition
problem, and rqmin is the minimum flow. It is the property of
all valid interblock means, Km, that, near the k1=k2 axis of the
(k1,k2)-space for any Dz,![]() . Approximate
means depart from Darcian as they depart from the k1=k2 axis.
. Approximate
means depart from Darcian as they depart from the k1=k2 axis.
To demonstrate this, we plot log(Ki/Kv) versus log(k1/k2). Wet-over-dry conditions are to the left of log(k1/k2) = 0, and dry-over-wet to the right. As Ki deviates from the true Darcian mean, Kv, log(Ki/Kv) deviates from zero.
Results
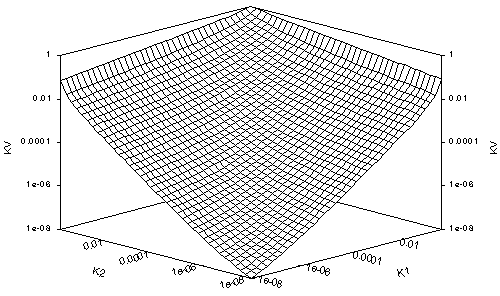
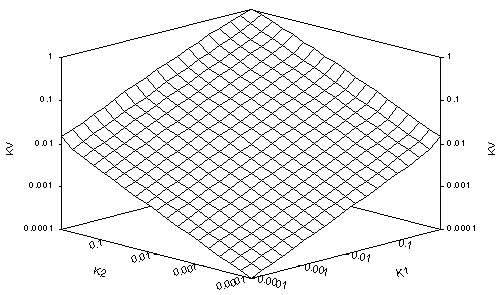
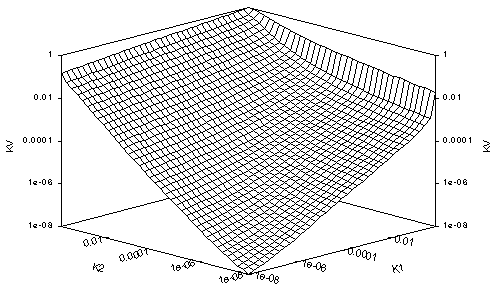
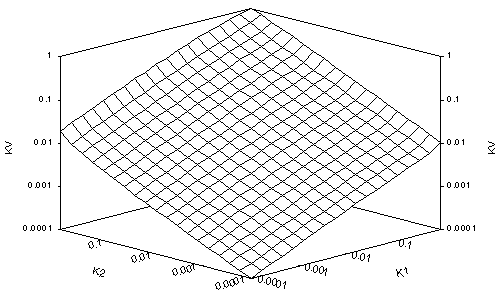
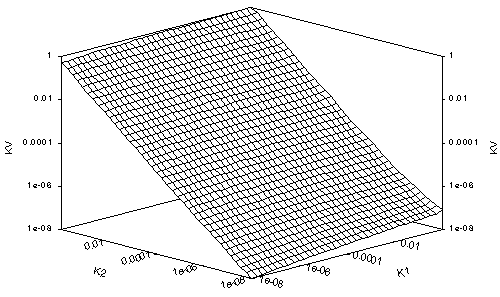
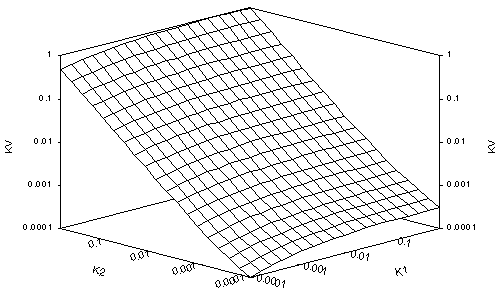
Figures 1a-d and 2a-d show the surface plots of the true Darcian means, Kv, for the fracture and matrix flows, respectively, for Dz = 0.01 yd, yd, 10 yd and 100 yd, in a-d respectively. All the plots look up the k1=k2 axis from small (10-8 or 10-4, dry) values, with the k2-axis increasing from dry to 1 (wet) on the left, the k1 axis increasing from dry to wet on the right and Kv increasing from dry to 1 vertically. The plots of Kv for small Dz are not far from Kh for each medium type. Each series shows how Kv transforms from Kh to k2.
Notice that when Kv approaches Kv in these cases, the surface plots curl upwards where either k1 or k2 approach saturation. This is typical of the van-Genuchten-style relation and is related to the rounded shoulder of the (log(y), log(kr)) plot of the relation near saturation. Notice that except for this slight shoulder, the Kv plot for the matrix flow for small Dz seems to approximate a geometric mean. This is typical of relations for which h approaches 2, and may account for the use of geometric means for fine-textured soils.
The value of yd = 33 m for matrix flow seems extreme, but comes from Table 3-12a for Unit 3 in Schenker, et al. (1995). It causes kr(y=153m, or 15 bar) = 0.0446. For matrix flow, log(k1/k2) thus varies from -1.35 to +1.35 over a 15-bar range. At the other extreme, for fracture flow, yd = 0.082 m comes from Table 3-32 in Schenker, et al. This causes kr(y=0.803m, or 0.079 bar) = 10-8, orders of magnitude from 15 bar, a value of matric suction normally taken for range in which soil water is immobile, except for vapor flow. Therefore, in plots of 10-8 < kr < 1, the full range of matric suction is not represented for fracture flow, while for plots of 10-4 < kr < 1, the matrix flow has been taken to absurdly high matric suctions at the dry end. Although kr = 10-8 seems a reasonable cutoff for considering interblock means in most cases, the reader should compensate accordingly. In addition, a step size of Dz = 3.3 km for matrix flow is a massive oversize, but still serves to illustrate the transition of Kv from Kh to k2 over a wide dynamic range. It makes apparent that choice of appropriate approximations to true Darcian means must be considered separately for each soil type.
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
For this study of Ki/Kv, wv in [7] is calculated from the routine in Listing 1, and the integral form of Kh in [7] is calculated by single-segment, 10th-order Gaussian quadrature (GQ), using the routine in Listing 2, adapted from Press, et al. (1989). The elliptic boundary condition method used for Figures 1 and 2 uses a similar routine for Kh, but with many composite segments to achieve much greater accuracy at a cost of much greater computational effort. The reader may verify against composite 10th-order GQ that single-segment 10th-order GQ is suitable for approximating Kh in fracture flow over |log(k1/k2)| < 8, and in matrix flow over |log(k1/k2)| < 3. Fourth-order GQ is suitable for Kh in fracture flow over |log(k1/k2)| < 3, and in matrix flow over |log(k1/k2)| < 1.5. No doubt other approximations are possible.
The variables p1 and p1 are the matric suctions, y1 and y2, at the centers of vertically adjacent grid cells. The function, ptc(p), returns the relative conductivity, kr, for a given matric suction, p > 0. The calculated value of Kh is the returned function value, dink10. There is not apparent division by Dy in the routine because it cancels the dy term in single-segment numerical integration.
double precision function dink10 (p1, p2)
implicit real*8 (a-h, k, o-z)
dimension g(5), w(5)
data (g(i), i=1,5) / 0.1488743389d0, 0.4333953941d0,
+ 0.6794095682d0, 0.8650633666d0, 0.9739065285d0 /
data (w(i), i=1,5) / 0.2955242247d0, 0.2692667193d0,
+ 0.2190863625d0, 0.1494513491d0, 0.0666713443d0 /
if (p1 .eq. p2) then
dink10 = ptc(p1)
return
end if
dink10 = 0.d0
pm = .5d0*(p1+p2)
pr = .5d0*(p2-p1)
do i = 1, 5
pg = pr*g(i)
dink10 = dink10 + w(i)*( ptc(pm+pg) + ptc(pm-pg) )
end do
dink10 = 0.5d0*dink10
return
end
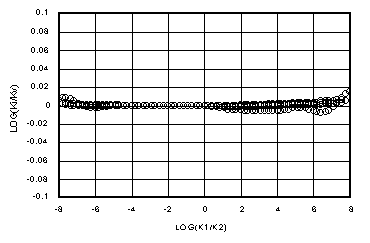
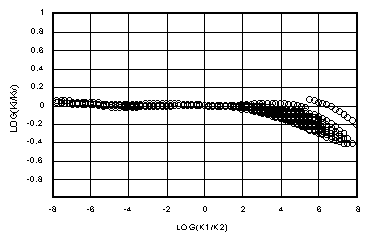
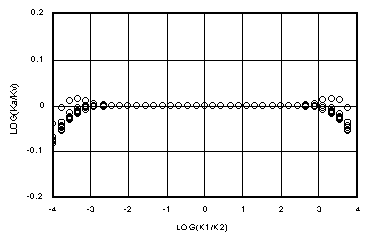
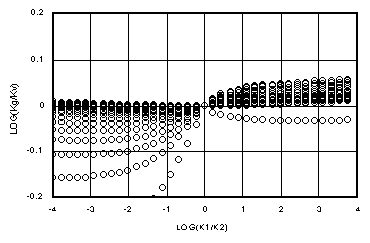
The remaining inaccuracy in Ki comes from applying a wv derived from an exponential relation for kr(y) [2] to a van-Genuchten-style relation [8]. Figures 3a-d demonstrate the total error in the Darcian Integral Mean approximation, Ki, for fracture flow, compared to the true Darcian mean, Kv , by plotting log(Ki/Kv) versus log(k1/k2) for Dz = 0.01 yd, yd, 10 yd, and 100 yd (a-d, respectively). Note the change of vertical scales from plot to plot. Figure 3b shows the worst error of the series, with Ki significantly smaller than Kv for dry-over-wet conditions where k1 is near 1 (the single line of points dipping down on the right, while the others raise up). The best fits of Ki to Kv are of course in the limits where Kv approaches Kh (small Dz) and where Kv approaches k2 (large Dz). It is the transition region in between that is more difficult to approximate.
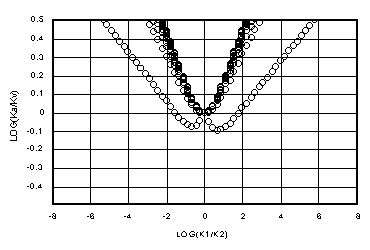
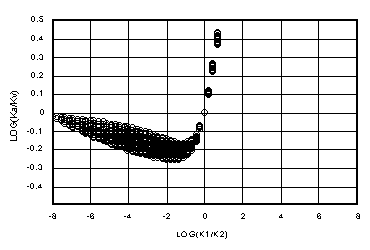
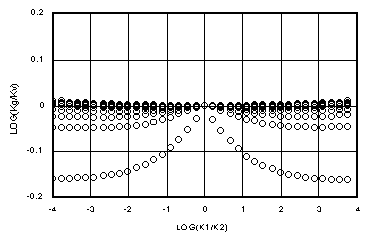
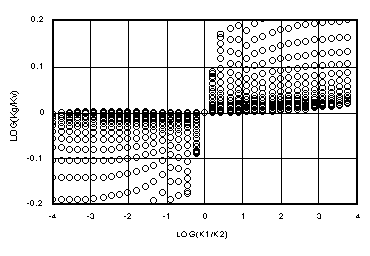
By comparison, Figures 4a-d show the ratio of the arithmetic mean, Ka = (k1+k2)/2, to Kv for all the same points. Notice that Ka in every case departs from the ideal, log(Ka/Kv) = 0, much faster than does Ki. The "flat" region where Ki conforms to Kv is much wider than for Ka, for which the flat region is vanishingly small, if it does exist. Notice that for large Dz (100 yd) in Figure 4d, Ka is about 1/2 of Kv for wet-over-dry. Previous work (Baker, et al., 1998b) demonstrated how this leads to a mass infiltration error of up to 50% in such cases.
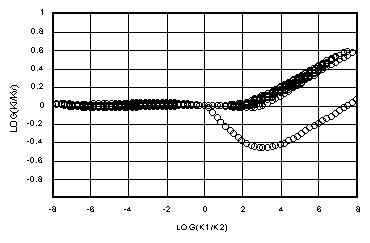
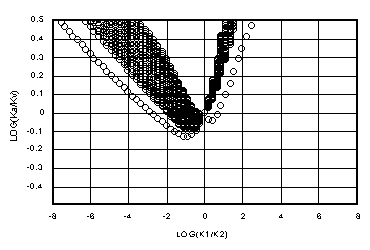
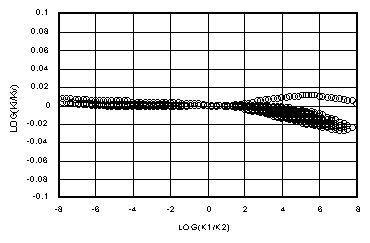
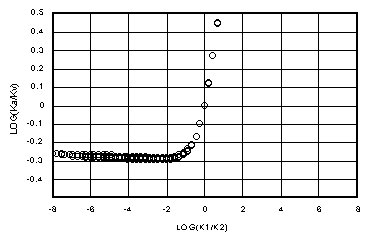
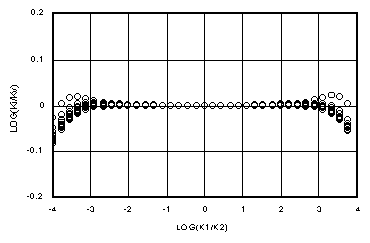
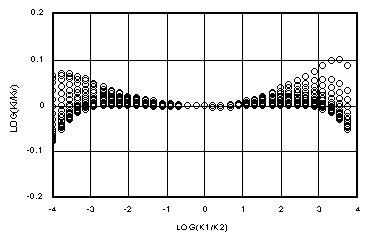
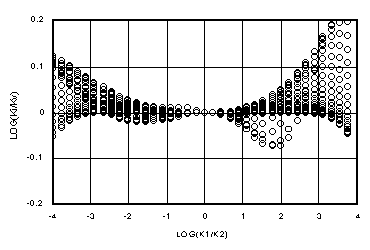
Figures 5a-d show log(Ki/Kv) versus log(k1/k2) for matrix flow for Dz = 0.01 yd, 0.1 yd, yd and 10 yd. The 3300 m space steps have been ignored as unlikely to be used. Figures 6a-d show the corresponding plot of log(Kg/Kv), where Kg = (k1*k2)1/2, the geometric mean. Again, in every case, Ki holds to the ideal farther from the k1=k2 axis than Kg. Figures 6a and b show how the geometric mean is reasonably close to Darcian except where one of the adjacent cells is near saturation. Kg becomes more unreliable in the transition region of Kv between Kh and k2, as shown in Figure 6c. In Figure 6d, it is apparent from Figure 2c that the only agreement between Kg and Kv comes for conductivities well below those at the 15 bar level.
We do not discuss the upstream mean here. Previous work (Baker, 1998a; Baker, et al., 1998b) has shown that the upstream mean is Darcian only for downwards flow and space steps significantly larger than yd, where Kv approaches k2. But for infiltration into moderate to coarse textured soils where Kg is not appropriate, the k2 mean remains a viable candidate, which the reader can investigate with the Darcian Integral Mean approximation presented here.
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|
Conclusions
The cases offered show the inaccuracies inherent in applying a Darcian weighting function, wv, developed from an analytic solution to an exponential conductivity relation to any other relation. They make the Darcian Integral Mean, Ki, a less than perfect approximation of true Darcian means. But for vertical space steps smaller than "displacement pressure" length, yd, it is nearly perfect over four to six orders of magnitude in the ratio of adjacent cell conductivities, k1/k2, depending on circumstances. For space steps of yd or greater, this approximation becomes increasingly less accurate for Topopah Spring welded tuff matrix flow, where the geometric mean is sometimes appropriate, but far outshines the geometric mean in the cases presented. For Topopah Spring welded tuff fracture flow, the main inaccuracies of the Ki approximation are significant only for dry-over-wet conditions, and then only in comparison to wet-over-dry conditions. In all of the presented cases for fracture flow, the arithmetic mean is orders of magnitude less Darcian than the Ki approximation.
It remains to be seen whether or not the extra computational overhead for the Ki approximation will outweigh its greater accuracy in general use. But it is a suitable tool for those who wish to examine the use of Darcian means in running models, without the overwhelming computational burden of the elliptic boundary condition (EBC) approach to generating true Darcian means. While the EBC method and an interpolation table would likely be more efficient for calculating true Darican means for an invariant unsaturated conductivity relation, the Ki approximation would likely be better for variable media. The reader is cautioned, however, not to make any assumptions beyond the current presentation without verification in the EBC method for a particular unsaturated conductivity relation.
Data Sets
Excerpts of the two ASCII data sets offered here, fracture.txt and matrix.txt, are shown below. Each file begins with a title line, a parameter line, a column header line and a blank line, followed by the columnar data with 1369 rows of information. The parameter line show the parameters for equation [8] above, with psid for yd, beta for b and eta for h. The columnar data is k1, the lower cell relative conductivity, k2, the upper cell relative conductivity, Kh, the horizontal or vertical diffusive Darcian mean for (k1,k2) (the integral for in [4]), and Kv, the total Darcian mean for vertical flow [1], for Dz = 0.01 yd, 0.1 yd, yd, 10 yd and 100 yd. In many PC browsers, one can right-click on the link and save the link as a file, which downloads the file to your hard drive.
(fracture.txt)
Fracture flow Darcian means
psid = 0.082m, beta = 4.23, eta = 8.075
k1 k2 Kh Kv(.00082) Kv(0.0082) Kv(0.082) Kv(0.82) Kv(8.2)
1.001E-08 1E-08 1.0005E-08 1.0005E-08 1.00049E-08 1.00043E-08 1.00012E-08 1.00001E-08
...
(matrix.txt)
Matrix flow Darcian means
psid = 33m, beta = 1.793, eta = 1.9825
k1 k2 Kh Kv(0.33) Kv(3.3) Kv(33) Kv(330) Kv(3300)
1.001E-08 1E-08 1.0005E-08 1.0005E-08 1.0005E-08 1.0005E-08 1.0005E-08 1.0005E-08
...
Acknowledgements
The original impetus for this approach came from unfunded Dissertation
work (Baker, 1994), expanding on Warrick (1991). A Phase I Small
Business Innovation Research grant from the U.S. Department of
Energy, Award No. DE-FG02-97ER82329, provided support and equipment
to further develop the concepts (Baker, 1998a). Subsequent work
has not been funded by any outside agency.
References
Baker, D.L., 1994. Improved algorithms for finite difference modeling of Richards' equation. Ph.D. Dissertation in Soil Physics, Agronomy Dept., Colorado State University, Ft. Collins, CO 80523, Summer 1994. (Also available through University Microfilms, Inc.)
Baker, D.L. 1995. Darcian weighted interblock conductivity means for vertical unsaturated flow. GROUND WATER, v. 33, no. 3, pp. 385-390.
Baker, D.L. 1998a. Developing Darcian means in application to Topopah Spring welded volcanic tuff. Report DOE/ER/82329-2 to the U.S. Department of Energy, June 1998, 118p.
Baker, D.L., M.E. Arnold and H.D. Scott, 1998b, Some analytic and approximate Darcian means, accepted by GROUND WATER, 12/10/98.
Celia, M.A., E.T. Bouloutas and R.L. Zarba. 1990. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. v. 26, no. 7, pp. 1483-1496.
Haverkamp, R., M. Vauclin, J. Touma, P. Wierenga and G. Vachaud. 1977. Comparison of numerical simulation models for one-dimensional infiltration. Soil Sci. Soc. Am. J. v. 41, pp.285-294.
Press, W.H., B.P. Flannery, S.A. Teukolosky and W.T. Vetterling, 1989, Numerical Recipes, The Art of Scientific Computing (FORTRAN Version), Cambridge Univ. Press, Cambridge, ISBN 0-521-38330-7, 702p.
Schenker, A.R., D.C. Guerin, T.H. Robey, C.A. Rautman and R.W. Bernard, 1995, Stochastic hydrogeological units and hydrogeologic properties development for total-system performance assessments, Sandia Report SAND94-0244 * UC-814, Prepared by Sandia National Laboratories, Albuquerque NM 87185 and Livermore CA 84550 for the United States Department of Energy under Contract DE-AC04-94AL85000, 87p + appendices.
Warrick, A.W. 1991. Numerical approximation of Darcian flow through unsaturated soil. Water Resour. Res. v. 27, no. 6, pp. 1215-1222.
Internet References
[1] Aquarius Engineering.