Note

This paper demonstrates the mathematical development of a 1-D numerical model for rapid infiltration into a physically heterogeneous soil with a transpiring crop. It uses mass-conserving, adaptive, diagonally-implicit, Runge-Kutta methods for time stepping, and Darcian means for intergrid unsaturated conductivity estimates. Some of the Fortran program variables used here are also defined in the I/O and Common specification of the model in Appendix A. The program listing for the code involving the flow of soil water is in Appendix B. The reader should look there for references to subroutines and functions in this text. This text often uses the Fortran variables from the program bnmf2v.for instead of standard Greek symbols for hydraulic parameters, in an attempt to help the reader relate the equations describing soil water flow to the Fortran code.

Topics

• Soil Characteristics
• Model Grid
• The DIRK2 Time Stepping Method and Newton's Method
• The Upper Boundary Condition
• The Lower Boundary Condition
• The Mass-Balance Criterion and Under-relaxation
• Adaptive Time-Stepping
• Root Water Extraction
• Intergrid Hydraulic Conductivity Means
• Comparisons
• Calibration Methods
• Files Available for Download
• References
• research home

Soil Characteristics (up)

In this model (bnmf2v.for) the soil is assumed to conform to a saturation relation [1] and a hydraulic conductivity relation [2], where the parameters, q_s (ths in the model), q_r (thr in the model), at, vm, vn, sc and bc are allowed to vary from grid point to grid point in the profile. Tables 1a-b show one set of such variation with depth. Although these data were fitted to field soil hydraulic measurements (Thiesse, 1984) obtained using the plane of zero-flux method (Arya, et al., 1975), one may clearly dispute whether these fits are accurate, especially for the displacement pressure, at. (Note: later work found that the number of parameters in this form overspecifies the data. Another form with fewer parameters was chosen for later work.) Nevertheless, they form a starting point and example set for the analysis. Note that z is positive downwards from the soil surface. Since the model grid is much finer than the experimental estimates, these data were fitted to the model grid by linear interpolation, producing a parameter value for each model grid point. A water table is assumed to exist at a depth of 5000 cm (50 m) down, and the soil characteristics are assumed to be uniform from the lowest field measurement to the water table.

Model Grid (up)

Figure 1 shows the model grid for the profile. The depth index, i in z(i), goes from 0 at the soil surface, z(0) = 0, to n+1 at the assumed water table, z(n+1) = zl. During infiltration, the height of the ponded water is zr (cm) above the soil surface. The separation between all points but the boundary points and those closest to them is dz (cm).

Figure 1: Model Grid for the Flow Code

The separation between z(0) and z(1) is dz/2. Thus, the upper boundary of the "cell" centered on z(1) is at the soil surface. This allows the hydraulic condition at the soil surface to be specified as a flow boundary. During infiltration, z(0) can be calculated to be the falling head of the ponded water as it evaporates, qe (cm/h) and infiltrates, qin (cm/h). When there is no infiltration, z(0) can be calculated to agree with the evaporation flux, qe.

The input value of the bottom of the model soil column, z(n) = cl, is modified by the program to fit this offset grid. First, the number of modeled grid cells, n, is set according to [3a], then cl is recalculated according to [3b]. The boundary between z(n) and z(n+1) is not centered. The bottom cell, centered on z(n) = cl, is assumed to be only dz long, with its bottom boundary dz/2 below the grid point. This offset grid also makes the effect of the outflow due to root extraction, rx (cm³/(cm³-h)), consistent from point to point. The roots are assumed to end at the bottom of the nth cell, z = cl + dz/2, with no extraction below that depth.

The DIRK2 Time Stepping Method and Newton's Method (up)

POULIT uses a second order diagonally-implicit Runge-Kutta (DIRK2) time stepping method (Baker, 1993, 1995) to solve Richards' equation [4] via finite differences. It belongs to a family of such methods that includes the common first-order Euler implicit (DIRK1) and second-order Crank-Nicolson methods as special cases. Equation [5] shows the finite difference formulation for the DIRK1 method, where the analytic variables have been replaced by Fortran variables at specific grid point indices, i.

In [5] the j in thj indicates the volumetric water content at the last calculation time, t_j = t_j+1-dt. The remaining variables are considered to be at the current time, t_j+1. While it is not practical to solve [5] with cv or rx at the j+1 time level in one step, it is achieved in the limit by lagging cv one iteration back in Newton's method for systems (Burden and Faires, 1985). Thus, cv(i) and rx(i) are recalculated at every iteration with the latest values for p(i) and p(i+1). After an arbitrary number of iterations, they theoretically approach the j+1 time level to an arbitrary degree (if the method is stable and convergent). However, in practice, numerical roundoff errors generally limit the level of convergence to a small, finite number that is difficult to predict. Target values of convergence may be anywhere from 10^-4 to 10^-10 in relative global mass balance, depending on the application.

The object of Newton's method is to drive a system of equations [5], f_i = 0, i=1,n, to zero on both sides. At the upper and lower boundary conditions, i = 1 and i = n, the equations f_i are modified, as we shall see. In this case, Newton's method solves for the entire grid of hydraulic pressure heads, p(i), simultaneously [6a], where J is the (n x n) Jacobian matrix, Dp is the (n x 1) pressure head correction vector, f is the (n x 1) mass balance vector, p_m+1 is the (n x 1) pressure head vector of the current iteration, and p_m is the (n x 1) pressure head vector of the last Newton iteration. The Jacobian is simply the tri-diagonal matrix set of partial derivatives of f(i) with respect to the p(i) that constitute it [6b]. All of the other terms of J are zero.

Each system equation, f_i, is determined by three independent variables, p(i-1), p(i) and p(i+1). Thus there are only three diagonals in the Jacobian. Between the boundary conditions, i = 2 to n-1, the form of the Jacobian is determined by one set to three equations [7a-c]. This is the simplest possible Jacobian, where only the terms of th(i), p(i-1), p(i) and p(i+1) are differentiated. In the DIRK1 method, the system of equations in [6] is solved by matrix inversion, in the model subroutine dgtsl (n, aa, bb, cc, r, info), where n is the number of solution variables, aa(i) is the lower diagonal array [7a] in [6], bb(i) is the diagonal array [7b], and cc(i) is the upper diagonal array [7c]. The array r(i) are the elements -f_i on input to the subroutine and the correction terms, Dp_i, on return.

The DIRK2 method solves two such problems in sequence in such a way as to minimize the error due to time step size, dt, to second-order effects. The first step solves a DIRK1 finite difference equation [8a] for a partial time step, pdt = prk*dt, 0 &pound; prk < 0.5 (the stable range). The next step solves at the full time step, dt, by combining information from the partial and full time steps [8b] with the weighting parameters, a1 and a2, such that a1 + a2 = 1. This implies that one must save the cv, p, ht and rx variables at the j+p time level to apply in [8b]. This can be avoided by rearranging equation [8a] and substituting into [8b] to get [8c], in which only the thp(i) array must be saved from the j+p time level. Note that the curly brackets in [8b] and [8c] are used not as matrices, but to collect terms on the right hand side for addition.

In this method the Jacobian for the partial and full time steps are constructed similarly to [7a-c]. For the partial time step, the interior Jacobian terms are shown in [9], where ra = dt/dz². For the full time step, the Jacobian terms are shown in [10]. The j+p and j+1 superscripts indicate that the ch(i) and cv(i) nonlinear coefficients are raised to those time levels for calculation by iteration in Newton's method.

[9]

[10]

Schwarz (1989) indicated that to find the finite method discretization error, one substitutes the analytic functions, such as p(z,t), p(z-dz,t+dt), p(z,t+dt), and p(z+dz,t+dt) into the locations in the finite difference method corresponding to their discrete values, and apply the Taylor series expansion. One can do this with [8b] and a symbolic mathematics package, such as Maple V Release 4 (tm Waterloo Maple, Inc.). The terms of dt, dt² and dt³ (without dz), etc., are collected and those which balance [8b] are eliminated. The remaining terms involve the three Runge-Kutta parameters, prk, a1 and a2, and a constant. Setting those terms equal to zero produces the Runge-Kutta parameter equations [11a-c].

For a linear advection-diffusion equation, solving all three equations in [11] produces a method that is theoretically third-order, with prk = 1/3. But for the nonlinear Richards' equation, a value of prk = 0.4 to < 0.5 is typically more accurate, depending on conditions. If prk is taken as a variable in the DIRK2 method, then [9] reduces to [12]. Note that for prk = 0, (a1,a2) = (1,0) produces the first-order explicit method, (a1,a2) = (0,1) produces the DIRK1 method, and (a1,a2) = (1/2, 1/2) produces the Crank-Nicolson method from [11]. In a simple linear diffusion problem (Baker, 1993), the Crank-Nicolson method is typically the most oscillatory of the DIRK2 methods. This model uses prk = 0.4.

Subroutine pwater in this model calculates the partial time step according to [8a]. Subroutine water then calculates the full time step according to [8c]. Both are called by subroutine compute, which calculates each time step.

The Upper Boundary Condition (up)

The flow of water into or out of the top of the soil column is qin (cm/h), positive downwards. If there is no infiltration, qin = -qe, the evaporation outflow. The evaporation, qe (cm/h), is determined in subroutine etrx. It is the lesser of the daily potential surface evaporation rate, sev (cm/h), or the conductivity of the soil surface, ck(0) (cm/h). The variable sev is determined from the daily total potential evapotranspiration, pet(klm) (cm), which is determined elsewhere, in the weather code. (klm is the weather-day index for the time series data)

For conditions of evaporation only, the upper boundary condition at z = 0, is set to constant flow in each time step [13a,b] at the top of the cell centered on z(1) = dz/2. The soil surface hydraulic pressure, p(0), and water content th(p(0)), are determined [14] by setting p(0) to the value needed to produce qe given ht(1). The Jacobian terms for the j+p time level [15a] and the j+1 time level [15b] are determined accordingly.

If the weather code reads a datum that produces enough rainfall for daily infiltration, xinfl(klm) (cm), a ponded head, zr, is instantly created in the next time step after midnight [16]. This head evaporates and drains away according to equation [17]. This ordinary differential equation is linked to the rest of the model by cv(0), ht(1) and qin.

It is convenient and practical to calculate the fall of zr in a two-step fashion on the same partial and full time steps as the flow. We can postulate a similar second-order implicit method [18a,b], where the ponded head is calculated at the partial time step level, zrp or zr^j+p, and full time step level, zr or zr^j+1, from the last time step level, zrj or zr^j. Both equations are functionally explicit in zrp and zr, and can be solved for them, as in [19a,b]. The soil surface inflows, qinp = qin^j+p, and qin = qin^j+1 (cm/h), are then calculated from the ponded head and ht(1) [20a,b].

The Jacobian terms must now be different. The boundary condition is essentially one of head, with a separation of dz/2 from the z(1) point. Equations [21a,b] show the mass balance functions that Newton's method reduces to zero at the upper BC. Equations [22a,b] show the resulting Jacobian terms.

[21a]

[21b]

[22a]

[22b]

In the transition from ponded infiltration with evaporation, to evaporation only, the equations change yet again. If the equations for ponded infiltration are used in the time step where the transition occurs, the account of water volume transferred to the soil will be inaccurate. Therefore, the program must extrapolate the likely transition point in the subroutine that calculates the partial time step, pwater. In addition to equation [19a], the subroutine pwater calculates [23]. If the equations predict either zrp or zr to be less than zero, then the program assumes that the remaining pond drains into the soil profile at a constant rate over the entire time step, less the evaporation rate [24]. The Jacobian terms for a flow boundary [15] are used, where the flow is described by [24].

The Runge-Kutta parameters a1 and a2 for the ponded head equations, [17] and [18], are coincidentally the same functions of prk as [12]. Listing 1 below shows the Maple V worksheet used to generate the Runge-Kutta parameter equations. The right-hand side of the second line is assumed to be zero and eliminated from the results of the third line. This leaves the Runge-Kutta parameter equations. If the reader uses this method, the reader will notice that the equation for the dt³ term, corresponding to [11c], has a right-hand-side of 1/6 instead of 1/3. The Runge-Kutta equations for the method in [8] can be constructed in similar fashion, except that the multi-variable function, mtaylor, must be used on dt and dz.

The Lower Boundary Condition (up)

By contrast, the lower boundary condition is quite simple. It is assumed that a water table or other condition of constant head, pl (cm), exists at depth, zl (cm). For this model (zl, pl) = (5000, 0). The cell at z(n) is assumed to be of size dz, with the lower cell boundary at dz/2 below it, for the purposes of calculating root extraction. The mass balance function reduced in Newton's method is [25], where dzl = zl-cl, with Jacobian terms [26]. The model assumes the upstream mean, ck_n, across dzl, because dzl is assumed to be much larger than the displacement pressure. The soil is also assumed to be of constant hydraulic characteristics from cl to zl. The large distance to a water table pegs the lower boundary condition while allowing the soil column at z(n) = cl to drain at nearly the rate of gravity flow. This may be reasonable in a situation where the increased clay content in lower soil layers decreases conductivity and restricts flow farther down.

The Mass-Balance Criterion and Under-relaxation (up)

This method is mathematically the same as the modified Picard method (Celia, et al., 1990). Therefore, the convergence of Newton's method is calculated on the global mass balance. For the partial time step, in subroutine pwater, the net flow into the soil is balanced against the change in water content [27a] in res1 (cm). In some cases Newton's method cannot be resolved with res1 alone because of numerical round off errors. So, res2 (cm) [27b], the weighted sum of the absolute values of the pressure head corrections in Newton's method (see [6]) is combined with res1 in the geometric mean [27c] to produce the mass-balance residual for the partial time step, resp (cm).

At the full time step, res1 (cm) is modified [28a] to account for the Runge-Kutta method. The same formula for res2 (cm) is used, and re1 and res2 are combined in the geometric mean to produce the mass-balance residual at the j+1 time level, res (cm) [28b]. In this model, if both resp and res are smaller than the mass-balance criterion, then Newton's method is considered to have converged, and the next time step is taken. If either fail, then the time step fails and is forced to repeat with a smaller dt. The mass-balance criterion can be from 10^-4 to 10^-6 (cm), and is set in code (in this version).

If equation [6a] is used as written, it is sometimes possible for the value of resp or res to increase from one Newton's method iteration, m, to the next, m+1. Therefore, it is often advisable to start Newton's method using under-relaxation [29], where the change in pressure, Dp, is reduced by an under-relaxation factor, ur. During infiltration, ur is started at a value of 0.5, and allowed to increase to an over-relaxation value of 1.5 for successful reductions of resp or res. Otherwise, it starts at 0.8 and is allowed to increase to a value of 3.0.

Listing 2 shows the algorithm this model uses for under-and over-relaxation in Newton's method. It tries to ensure that the mass-balance residual, res (or resp), decreases with every iteration. If it does not, then the iteration is restarted with the ur cut by half, with a lower floor of 0.1. Model instabilities or numerical errors can cause ur to sit at 0.1 until the maximum number of iterations, maxit, has been reached. This failure is also noted by the program, which then decreases the size of the time step. (Note - later work, not presented here, found that when ur is reduced, a similar program tends to reduce it all the way to 0.1 and restart with a smaller time step anyway. The increasing trend of ur works well to stabilize the model, but the automatic reduction of ur does not work as well as hoped. Any insight that others may have into the reasons for this and possible corrections would be welcome.)

Adaptive Time-Stepping (up)

This version of POULIT changes the size of the time step to make sure that Newton's iteration finishes within the maximum number of iterations, maxit. It does this on the supposition that a larger time step will require more Newton iterations to converge, if at all, due to increased time step digitization errors. The converse supposition is that a smaller time step will fix the problem. This is not always true, but does work under most conditions.

Listing 3 shows the algorithm used in subroutines pwater, water and compute to adjust the time step by this method. In this listing, only the internal workings of subroutine water will be addressed. Subroutine pwater uses the same code to adjust dt.

In Listing 3, line 5 indicates that during infiltration, the size of the time step, dt, is limited. Every day begins with the time step set to the maximum size, dtt. It is appropriate in that if the size of the time step is likely to be longer than it takes to infiltrate the ponded water on a rain day, then the size of dt should be reduced. This avoids excessive reductions of the time step size to that which will pass the adaptive criteria of Listing 3.

If one assumes that the values of qe, cv(0) and ht(1) are correct at the beginning of the time step, and solves equation [17] analytically for time at which zr = 0, this produces the estimate for the end time of the infiltration, dtr [30]. If the ponded water is higher than 0.1 cm and ht(1) < 0, then dtr is used as the ceiling for dt.

Root Water Extraction (up)

Root extraction of the soil water takes the potential evapotranspiration apportioned to plant transpiration and distributes it among the roots according to the weighted product of the root distribution times the soil hydraulic conductivity, reduced by the root stress due to low soil water content, if any. The methods used in this version are sometime simple, and may not be applicable in all cases. The user can change them as seems fit.

This version of the model (bnmf2v.for) uses a simple ratio, etr, to apportion potential daily evapotransipration, pet (cm), to the plant transpiration rate, et (cm/h) [31]. Equation [32] shows a simplified root distribution curve, that at one time was more complicated [33]. The root stress factor, rst [34], denotes a reduced ability of the plants to take up water when it nears zero. As the water content at z(i), th(i), moves closer to the residual water content, thr(i), rst goes to zero. It is modified by the upper drainage limit, udl(i), which is in turn related to the displacement pressure, at(i). As a result, for finer soils, where at(i) tends to be larger, roots are less able to take up water than for coarser soils.

The root water extraction rate, rx(i) (cm³/(cm³-h)) [35], shows how the plant transpiration rate, et(klm), is distributed according to the root distribution, rdist(i), and the soil hydrualic conductivity, ck(i). At one time the root stress factor, rst, was used to calculate the root uptake reduction factor, etg, as a simple quadratic with a cutoff [36]. Since functions with discontinuities in the function or derivative can lead to model instabilities, it has been replaced with the Gompertz function [37] (Edelstein-Keshet, 1988).

The Gompertz function, with other constants, was chosen first because it made a reasonable fit to [36], while demonstrating continuity in the function and its derivatives over the range of rst. While the model still used [33] for the root distribution, equation [37] was calibrated to field measurements through the variables, etr in [31], rl in [33] and gk in [37]. A period from June 30, 1990 to August 30, 1990 was modeled, since it went from relatively wet soil conditions to a significant water deficit in the field data. It was assumed that as the dry conditions persisted, that the soil water deficit would be most affected by the plant uptake. The model soil hydraulic pressures at z = 30, 60, 90, 120 and 200 cm were compared to field readings averaged over two duplicates and six plots on August 29, 1990, by the sum-squared-error. The values of etr, rl and gk above produced the fits with the least sum-squared-error in the pressures. But since both the model and root distribution function have changed since then, it is possible that these values are no longer valid.

Intergrid Hydraulic Conductivity Means (up)

In order to calculate Darcy's law [38] between two grid points, z(i) and z(i+1), the intergrid hydraulic conductivity, cv(i), must first be estimated. The hydraulic conductivities, ck(i) and ck(i+1) are known at the grid points from the solutions to the heads at those points, but the intergrid mean must be calculated. The estimation method chosen here is one of the simpler of the so-called Darcian means (Baker, et al., 1999). This one assumes a homogeneous medium and applies the solutions to steady-state flow problems piecewise in time and space to transient flow problems.

This approach implies that the true mean conductivity is a weighted sum [39] of the up-gravity mean, ck(i), and the integral mean conductivity with respect to pressure head, kh [40]. Strictly speaking, the weighting function, wv(i) [41], applies only in a homogeneous soil when ck(i) = ck(i+1). It is increasingly inaccurate as the adjacent conductivities diverge. Nevertheless, this limited approximation does account in some fashion for the effects of gravity and space step size on the intergrid mean, as many of the standard, fixed-formula methods do not.

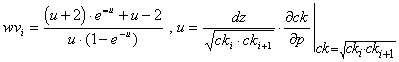
In this model, kh is calculated by 4th-order Gaussian quadrature in function dink. The intergrid mean, cv(i), is calculated in function dkmh, which is set up in subroutine wprop. Since equations [39] - [41] do not account for changing soil properties, wprop takes the arithmetic mean of the soil hydraulic parameters, saturated hydraulic conductivity (sc), hydraulic exponent (bc), displacement pressure (at), and the van-Genuchten exponents (vm and vn), from the values at the grid points, z(i) and z(i+1), and creates a fictitious average soil to be used between the grid points in [39] - [40]. Other investigators might wish to take the harmonic mean of the saturated conductivities, or some other such approach. But the soil parameters vary smoothly in the Captina soils investigated here. This approach is a reasonable starting point.

Comparisons (up)

There may be advantages in convergence to the fine-grid solution over a DIRK1 times stepping method using a DIRK2 method. But later work with this model (not presented here) determined that it is a slower method than DIRK1 and actually had a larger mass balance error for the same convergence criterion. Also, the adaptive time-stepping used, that adjusts the size of the time step for mass-balance error, tends to obscure any differences that otherwise would be found with fixed time steps. Thus the DIRK2 method was set aside in favor of the DIRK1 method for use in calibration trials of the model, since this use consumes many times more computing resources than prediction runs. No comparisons have yet been made. But as the DIRK1 model becomes more heterogeneous in soil characteristics in the course of calibration, it tends to fail to converge more often, as indicated by a cutoff limit of 1000 time steps per day. The run time also increases from about 25 seconds per 225 days on a fast workstation to 2 to 4 minutes. This is particularly noticeable for large infiltration events after long dry spells. It may be that returning to the DIRK2 method could improve the model performance, but this has not yet been tried. --9/8/2000)

Calibration methods (up)

(This work is not yet done at the time of this writing. Because of the long computing times necessary to calibrate a model to one growing season of data, the approach is necessarily minimalist. Currently, it is assumed that any discrepancy between measured soil characteristics from the field and laboratory and the calibrated characteristics can be described by a simple factor multiplying the parameter curve over the entire soil column. In this version, bnmf2v.for, the parameters atr, vnr, vmr, scr and bcr in the main program serve that function. In later versions, it has been necessary to consider more complicated approaches, such as a linear or quadratic change of the calibration parameters with depth. But, since this work is not yet complete, comment upon it will have to wait for another time. - 9/11/2000)

Example Files Available for Download (up)

• bnmf2v.for (86k) - a stripped-down version of POULIT limited to flow code
• come4.for (3k) - an include file with common statements, used in most subroutines
• appinfo.dat (1k) - an input file, w/ scs curve number and litter application information (if any)
• soils.dat (3k) - an input file of soil characteristics data
• sinit.dat (1k) - an input file of initial conditions
• weather.dat (1k) - an input file of rain and temperature data, from day 116 of 1991 to day 125
• outday.dat (1k) - an input file of measured soil column data, set not to affect this run.
• bnmf2v.zip (23k) - a zipped file of all of the above

Errata

If you find any, please let us know. mailto:dscott@cleora.uark.edu

References (up)