 |
 |
|
|
 |
Before the recent collapse of a major corporation, a Fortune magazine journalist rating the company's stock asked a simple question, "How do you make money?" In this business there is an equally simple question, "How do you do math?" Sometimes an assemblage of dimensionless variables is presented as a case of dimensional analysis, misapplying the Buckingham Pi theorem. The theorem, its usage and its limitations are reviewed in the context of water flow through a trapezoidal notch in a trapezoidal reservoir embankment (dam breach model).
The Buckingham Pi theorem may sometimes be misused as a general solution method for complex engineering problems. In his text, Applied Mathematics, Logan (1987) gives the example of its application to the expansion of the fireball of a nuclear explosion. In this case, there are four pertinent physical quantities expressed in three physical dimensions. According to the theorem, this leaves one possible dimensionless pi-variable to express the physical law of expansion, from which one can obtain r5p/(t2e) = constant, where r is the radius of the fireball, p is the atmospheric pressure outside the fireball, t is the time and e is the energy released in the blast. In this special case, the basic physical law, confirmed by later experiments, literally falls out of the non-dimensional analysis.
But it goes too far to say that all physical laws can fall out of non-dimensional analysis. Logan notes, "the existence of a physical law is an assumption. In practice one must conjecture which are the relevant variables in a problem and then apply the machinery of the theorem. The resulting dimensionless physical law must be checked by experiment, or whatever, in an effort to determine the validity of the original assumptions." Nor is it necessarily valid to take any particular pi-variable and construct a physical law by setting that variable equal to the general formula for pi-variables in a given problem.
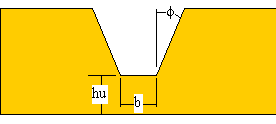
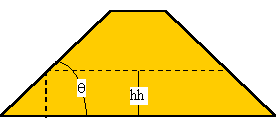
Take for example the case of water flowing in a trapezoidal
notch through the trapezoidal embankment of a reservoir. The notch
has a bottom width, b (units of length, L), at height, hu (L),
above the reservoir floor, with a sidewall slope angle of f (rad) from the vertical. The embankment
has an upstream slope angle of q (rad)
above the horizontal. The intersection of the notch with the upstream
slope is called the crest of the resulting flume or weir. In addition,
the floor of the notch downstream of the crest can be drop, hh
(L), below the crest, forming a rectangular channel below the
crest, so that the water flowing into it can be an aerated waterfall,
or nappe. The pictures below show one such condition with hh =
hu in the drawn figures and hh = 0 in the photograph of the plywood
model.
|
|
|
|
|
|
Suppose that one constructs, as did one widely-respected Research
Leader, a non-dimensional equation (1) to explain the flow, Q,
through the notch. Is it a legitimate construction of the Buckingham
Pi theorem and does it constitute a valid "physical law"?
(1) 
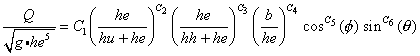, where Q (L3/T)
is discharge, g (L/T2) is the acceleration of gravity,
he (L) is the elevation head of the reservoir above the crest
behind the influence of the notch, hu, hh f and q are defined
as before, and C1 through C6 are dimensionless
fitting parameters.
According to Logan, the Buckingham Pi theorem says:
Let 
be a unit-free physical law that relates
the dimensional quantities q1, q2, …,
qm. Let L1, …, Ln (n <
m) be fundamental dimensions with dimension
,
i = 1, …, m. And let r = rank A, where A is the dimension
matrix (2). Then there exists m-r independent dimensionless quantities,
p1, p2,
…, pm-r, which can
be formed from q1, q2, …, qm,
and the physical law is equivalent to an equation 
expressed
only in terms of the dimensionless quantities.
(2)
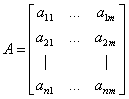, where aij are the power
variables of the dimensions Lj for each qi.
In many cases, r = n. The term "unit-free physical
law" only means that the dimensions of both sides of an equation
cancel out, so that one cannot set mass equal to length, for example.
Logan follows the theorem with a diffusion example which we
can follow. To determine whether or not sin(q)
and cos(f) are legitimate p-variables,
let us define three lengths:
dn = the depth (L) of the notch from the top of the embankment
to the horizontal crest
lu = the length (L) of the upstream slope from the crest to the
top of the embankment, such that sin(q) = dn/lu
ls = the length (L) of the inclined side slope of the trapezoidal
notch such that cos(f) = dn/ls
We now have nine physical variables, Q, g, he, b, dn, lu, ls, hh and hu, in terms of two dimensions, length (L) and time (T). Following Logan's example, we set up a dimension matrix to determine the power equations necessary to derive the dimensionless p-variables (3).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) pi = Qa1 ga2 hea3 ba4 dna5 lua6 lsa7 hha8 hua9 , where a1i, …, a9i is assumed
From (3) we set up the equation for the dimensions of the p-variables (4). This leads to the equations (5) and (6), which must be satisfied simultaneously to produce dimensionless p-variables. Equation (5) can be satisfied only by a1 = a2 = 0 or a2 = -a1/2. If the second choice is taken, and we set a1 = 1, then equation (6) becomes (7), and a2 = -1/2. We can set a4 = … = a9 = 0, which with (7) produces the (8) and the left hand side of (1), which is a valid p-variable, p1.
(4) dimension[pi] = T(-a1-2a2)
L(3a1+a2+a3+a4+a5+a6+a7+a8+a9)
(5) a1 + 2 a2 = 0
(6) 3 a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8 + a9 = 0
(7) (5/2)a1 + a3 + a4 + a5 + a6 + a7 + a8 + a9 = 0
(8) p1 = Q/(g he5)1/2
It is obvious from (4), (5) and (6) that the rank of the A matrix is r = 2, the same as the number if physical dimensions. We have m = 9, so we need m - r = 7 p-variables to completely specify the problem in dimensional analysis. Here we find the first dispute with equation (1); it only has 6 dimensionless variables. Suppose that we set a1 = a2 = 0, and work with (6) to get the remaining 6 p-variables. It can be shown that the following solutions form an independent set of 7 with p1:
p2 = b/he, p3 = dn/lu = sin(q), p4 = dn/ls = cos(f), p5 = he/hh, p6 = he/hu, p7 = he/dn
But there is no way with this method to generate the dimensionless variables (he/(hu+he)) or (he/(hh+he)). So equation (1) may be missing one p-variable and has two that are not valid. It is surely constructed of dimensionless variables, but it does not satisfy the Buckingham Pi theorem. Therefore it does not strictly illustrate an example of dimensional analysis. One should note that it may be possible to argue that when he < dn, the depth of the notch, dn, should have no effect on the flow. Therefore, one could dispense with p7. But if he > dn, then the flow overtops the embankment and p7 becomes necessary, as may other variables.
There is nothing about the Buckingham Pi theorem that requires a physical law to be a product of powers of p-variables. This approach seems merely to imitate equation (3) and does not guarantee a valid physical law according to the theorem. The theorem only guarantees that if a physical law exists, then the terms can be rearranged into m - r dimensionless p-variables.
One can see this by considering a known solution (approximate, ignoring secondary effects such as boundary layers) to a special case to the current problem (Fread, 1988). If the downstream floor of the notch is level with the horizontal crest, hh = 0, then the broad-crested weir equation (9) applies, where the dimensions of the coefficients c0 and c1 are the same as the square root of gravity, g (L/T2).
(9) Q = c0 b he3/2 + c1 tan(f) he5/2 , where c0 = 3 (L1/2/T) and c1 = 2 (L1/2/T)
The he3/2 term comes from flow over the horizontal floor of the notch and the he5/2 term comes from flow over the inclined sides of the notch. We can consider the tan(f) term to be a dimensionless coefficient and leave it out of the dimensional analysis on the basis that he < dn. Notice that equation (9) has two terms while equation (1) only has one. Since (9) has been confirmed by both theory and experiment, one can take the five physical variables, Q, b, he, c0 and c1, and construct a valid dimensionless equation with m - r = 3 p-variables, such as:
(10) 
, where
However, as (10) demonstrates, merely having a dimensionless equation
does not guarantee any greater understanding. If an equation like
(9) is correct and works properly at different physical scales,
an equation like (10) is no better or worse. It is only a rearrangement
of the terms. If (1), or any mathematically equivalent variant
with dimensioned variables, cannot fit a known special case like
(9), then it cannot be true in general.
Dimensional analysis can not necessarily solve general problems, nor can it even add to understanding unless it is used to some legitimate purpose. In his exposition on subcritical and supercritical flow in rectangular channels, Henderson (1966) uses a dimensionless equation to collapse a family of curves of depth, y (L), versus specific energy, E (L) into a single line. Science is replete with examples where dimensionless variables make integrals go neatly from zero to one.
